علم الرجفات الشمسية

علم الرجفات الشمسية (هيليوسيسمولوجي) (Helioseismology) هو فرع من فروع الفيزياء الشمسية يهتم بدراسة انتشار موجات الضغط والتذبذبات التي تحدث على سطح الشمس واستنتاج البنية الداخلية والحركية للشمس من انتشار الموجات الزلزالية، وخاصة الموجات الصوتية (موجات p) وموجات الجاذبية السطحية (موجات f).[1]

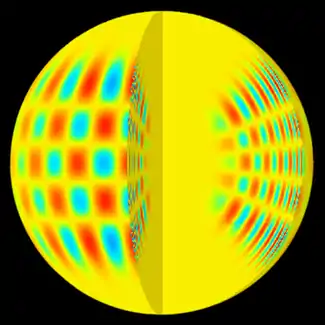
صورة مولدة حاسوبيا تظهر نمط التذبذب الصوتي الشمسي- P داخل وعلى سطح الشمس. (l=20, m=16, و n=14.) لاحظ أن الزيادة في سرعة الصوت عندما تقترب الموجات من مركز الشمس يسبب زيادة مقابلة في الطول الموجي الصوتي.

طور علم الرجفات الشمسية قياسا على علم الزلازل وبعد ذلك برز علم دراسة تذبذب النجوم ، حيث يتم تحليل الموجات الزلزالية لتحديد الهياكل الداخلية للنجوم الأخرى.[2] الفيزياء الأساسية في كل من علم الزلازل وعلم الرجفات الشمسية هي حركات الموجات النشطة داخل الجسم (الأرض أو الشمس) ولكن هناك العديد من الاختلافات في عدد ونوع الموجات لكل من البيئات الأرضية والشمسية. ولأن الشمس جسم مائِع لا يمكن أن تدعم موجات الجر ( موجات-s)، على عكس الموجات الزلزالية على الأرض.ويستثنى من ذلك الموجات المغناطيسية الصوتية التي تبدو مهمة فقط في الغلاف الجوي.[3]

الموجات الزلزالية

تتولد الموجات الزلزالية الشمسية من الاضطرابات في منطقة الحمل الحراري تحت سطح الشمس مباشرة وتتضخيم ترددات معينة من خلال التداخل البنائى، مما يؤدي إلى رنين. وبعبارة أخرى، فإن اضطرابات الشمس "ترن" مثل جرس. تنعكس موجات الرنين بالقرب من الغلاف الضوئي (السطح المرئي للشمس) حيث يمكن ملاحظتها. يمكن الكشف عن التذبذبات في أي سلسلة زمنية تقريبا من الصور الشمسية، ولكن من الأفضل رصدها من خلال قياس تأثير دوبلر لخطوط امتصاص الغلاف الجوي. وتكشف تفاصيل انتشار الموجات الزلزالية خلال الشمس، المستنبطة من الترددات الرنانة عن البنية الداخلية للشمس، مما يسمح للفيزياء الفلكية بوضع تمثيل مفصل للغاية للطبقات الهيدروستاتيكية[4] والسرعة الزاوية الداخلية.[5][6]ويسمح ذلك بتقييم عزم رباعي الأقطاب()[5] وعزوم ذات قيم أعلى[7]من قدرة الجاذبية السطحية للشمس .

المميزات
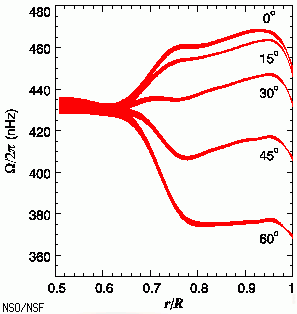
الدوران الداخلي للشمس يظهر دوران تفاضلي في الطبقة الخارجية لمنطقة الحمل الدوران منتظم تقريبا في مركز منطقة الإشعاع، ويسمى التحول بين هذه المناطق خط السرعة

تمكنت الهيليوسيسمولوجي من استبعاد احتمال أن مشكلة النيوترينو الشمسي كانت نتيجة لأنماط ثابتة غير مضبوطة من باطن الشمس[8] [9] [10] .وتشمل المميزات التي كشفتها الهيليوسميسمولوجي أن منطقة الحمل الحراري الخارجي والمنطقة الإشعاعية الداخلية تدور بشكل مختلف، والتي يعتقد البعض أنها تولد المجال المغناطيسي الرئيسي على الأقل في الطبقات الخارجية للشمس بواسطة تأثير الدينامو.[11][12]

بشكل عام، فإن السرعة الزاوية للمنطقة الحمل الحراري تنخفض من خط الاستواء إلى القطبين، والدوران الداخلي للشمس يظهر دوران تفاضلي في الطبقة الخارجية لمنطقة الحمل الدوران منتظم تقريبا في مركز منطقة الإشعاع، ويسمى التحول بين هذه المناطق خط السرعة[13][14]و منطقة الحمل الحراري لديها "تيارات نفاثة" من البلازما (تسمى التذبذبات التوائية) تمتد آلاف الكيلومترات تحت سطح .[15] تشكل التيارات النفاثة جبهات واسعة في خط الاستواء، وتنتقل إلى عواصف إعصارية أصغر عند خطوط العرض العالية. التذبذبات التوائية هي الاختلاف الزمني في الدوران التفاضلي الشمسي.وهي تناوبات مقيدة من دوران أسرع وأبطأ وحتى الآن لا يوجد تفسير نظري مقبول لها، على الرغم من ارتباطها بعلاقة وثيقة مع الدورة الشمسية ، كما أن لديها فترة من أحد عشر عاما، منذ أن رصدت لأول مرة في عام 1980 [16]

ويمكن أيضا أن تستخدم الهيليوسميولوجيا لتصور الجانب البعيد من الشمس عن الأرض، بما في ذلك البقع الشمسية. بعبارات بسيطة، البقع الشمسية تستوعب وتحرف الموجات الهيليوسميولوجية، مما يسبب قصور زلزالي عندما تواجه الغلاف الضوئي مرة اخرى .[17] ولتيسير التنبؤ بالطقس الفضائي، تم إنتاج الصور الزلزالية للجزء المركزي للجانب الشمسي البعيد تقريبا منذ أواخر عام 2000 من خلال تحليل البيانات من المركبة الفضائية سوهو، ومنذ عام 2001، تم تخيل الجانب البعيد بأكمله بهذه البيانات.

تأريخ هيليوسيسمولوجي

يمكن استنتاج عمر الشمس بواسطة الدراسات المتعلقة بالرجفات الشمسية.[18] [19] [20] [21] هذا لأن انتشار الموجات الصوتية في عمق الشمس يعتمد على تكوين الشمس، ولا سيما الوفرة النسبية للهليوم والهيدروجين في النواة. منذ أن بدأت الشمس بتحويل الهيدروجين إلى هيليوم طوال حياتها، الوفرة الحالية من الهيليوم في قلب الشمس يمكن استخدامها لاستنتاج عمر الشمس، وذلك باستخدام النماذج العددية للتطور النجمي المطبقة على الشمس (النموذج الشمسي القياسي). يوفر هذه الأسلوب طريقة للتحقق من عمر النظام الشمسي التي تم جمعها من التأريخ الإشعاعي للنيازك.

مصادر
  1. Deubner, F.L.; Gough, D.O. (1984). "Helioseismology: Oscillations as a Diagnostic of the Solar Interior". Annual Reviews of Astronomy and Astrophysics. 22: 593–619. Bibcode:1984ARA&A..22..593D. doi:10.1146/annurev.aa.22.090184.003113. الوسيط |CitationClass= تم تجاهله (مساعدة)
  2. Gough, D.O. (1975). "Beginnings of asteroseismology". Nature. 314: 14–15. Bibcode:1985Natur.314...14G. doi:10.1038/314014a0. الوسيط |CitationClass= تم تجاهله (مساعدة)
  3. Campbell, W.R.; Roberts, B. (March 1989). "The influence of a chromospheric magnetic field on the solar p- and f-modes". Astrophysical Journal. 338: 538–556. Bibcode:1989ApJ...338..538C. doi:10.1086/167216. الوسيط |CitationClass= تم تجاهله (مساعدة)
  4. ChristensenDalsgaard, J.; Duvall Jr., T.L.; Gough, D.O.; Harvey, J.W.; Rhodes Jr, E.J. (May 1985). "Speed of sound in the solar interior". Nature. 315: 378–382. Bibcode:1985Natur.315..378C. doi:10.1038/315378a0. الوسيط |CitationClass= تم تجاهله (مساعدة)
  5. Duvall Jr., T.L.; Dziembowski, W.A.; Goode, P.R.; Gough, D.O.; Harvey, J.W.; Leibacher, J.W. (July 1984). "Internal rotation of the sun". Nature. 310: 22–25. Bibcode:1984Natur.310...22D. doi:10.1038/310022a0. الوسيط |CitationClass= تم تجاهله (مساعدة)
  6. Schou, J.; Antia, H.M.; Basu, S.; Bogart, R.S.; Bush, R.I.; Chitre, S.M.; Christensen-Dalsgaard, J.; De Mauro, M.P.; Dziembowski, W.A.; Eff Darwich, A.; Gough, D.O.; Haber, D.A.; Hoeksema, J.T.; Howe, R.; Korzennik, S.G.; Kosovichev, A.G.; Larsen, R.M.; Pijpers, F.P.; Scherrer, P.H.; Sekii, T.; Tarbell, T.D.; Title, A.M.; Thompson, M.J.; Toomre, J. (September 1998). "Helioseismic Studies of Differential Rotation in the Solar Envelope by the Solar Oscillations Investigation Using the Michelson Doppler Imager". Astrophysical Journal. 505: 390–417. Bibcode:1998ApJ...505..390S. doi:10.1086/306146. الوسيط |CitationClass= تم تجاهله (مساعدة)
  7. Antia, H.M.; Chitre, S.M.; Gough, D.O. (January 2008). "Temporal variations in the Sun's rotational kinetic energy". Astronomy and Astrophysics. 477: 657–663. Bibcode:2008A&A...477..657A. doi:10.1051/0004-6361:20078209. الوسيط |CitationClass= تم تجاهله (مساعدة)
  8. Gough, D.O. (1991). "Seismic constraints on the solar neutrino problem". Annals of the New York Academy of Sciences. 647: 199–217. Bibcode:1991NYASA.647..199G. doi:10.1111/j.1749-6632.1991.tb32171.x. الوسيط |CitationClass= تم تجاهله (مساعدة)
  9. Bahcall, J.N.; Pinsonneault, M.H.; Basu, S.; Christensen-Dalsgaard, J. (January 1997). "Are Standard Solar Models Reliable?". Physical Review Letters. 78 (2): 171–174. arXiv:astro-ph/9610250. Bibcode:1997PhRvL..78..171B. doi:10.1103/PhysRevLett.78.171. الوسيط |CitationClass= تم تجاهله (مساعدة)
  10. Gough, D.O. (May 1999). "Helioseismology and solar neutrinos". Nuclear Physics B Proc. Suppl. 77: 81–88. Bibcode:1999NuPhS..77...81G. doi:10.1016/S0920-5632(99)00401-6. الوسيط |CitationClass= تم تجاهله (مساعدة)
  11. Thompson, M.J.; Christensen-Dalsgaard, J.; Miesch, M.S.; Toomre, J. (2003). "The Internal Rotation of the Sun". Annual Review of Astronomy & Astrophysics. 41 (1): 599–643. Bibcode:2003ARA&A..41..599T. doi:10.1146/annurev.astro.41.011802.094848. الوسيط |CitationClass= تم تجاهله (مساعدة)
  12. Ossendrijver, M. (2003). "The solar dynamo". The Astronomy and Astrophysics Review. 11 (4): 287–367. Bibcode:2003A&ARv..11..287O. doi:10.1007/s00159-003-0019-3. الوسيط |CitationClass= تم تجاهله (مساعدة)
  13. Spiegel, E.A.; Zahn, J.-P. (November 1992). "The solar tachocline". Astronomy and Astrophysics. 265: 106–114. Bibcode:1992A&A...265..106S. الوسيط |CitationClass= تم تجاهله (مساعدة)
  14. Gough, D.O.; McIntyre, M.E. (August 1998). "Inevitability of a magnetic field in the Sun's radiative interior". Nature. 394: 755–757. Bibcode:1998Natur.394..755G. doi:10.1038/29472. الوسيط |CitationClass= تم تجاهله (مساعدة)
  15. Vorontsov, S.V.; Christensen-Dalsgaard, J.; Schou, J.; Strakhov, V.N.; Thompson, M.J. (April 2002). "Helioseismic Measurement of Solar Torsional Oscillations". Science. 296 (5565): 101–103. Bibcode:2002Sci...296..101V. doi:10.1126/science.1069190. PMID 11935019. الوسيط |CitationClass= تم تجاهله (مساعدة)
  16. Howard, R.; Labonte, B.J. (July 1980). "The sun is observed to be a torsional oscillator with a period of 11 years". Astrophysical Journal. 239: L33–L36. Bibcode:1980ApJ...239L..33H. doi:10.1086/183286. الوسيط |CitationClass= تم تجاهله (مساعدة)
  17. Lindsey, C.; Braun, D.C. (March 1990). "Helioseismic imaging of sunspots at their antipodes". Solar Physics. 126 (1): 101–115. Bibcode:1990SoPh..126..101L. doi:10.1007/BF00158301. الوسيط |CitationClass= تم تجاهله (مساعدة)
  18. Dziembowski, W.; Fiorentini, G.; Ricci, B.; Sienkiewicz, R. (1999). "Helioseismology and the solar age". Astronomy and Astrophysics. 343: 990–996. arXiv:astro-ph/9809361. Bibcode:1999A&A...343..990D. الوسيط |CitationClass= تم تجاهله (مساعدة)
  19. Gough, D. (2001). T.von Hippel, C. Simpson and N.Manset (المحرر). "Lessons Learned From Solar Oscillations". Astrophysical Ages and Times Scales. 245: 31–43. Bibcode:2001ASPC..245...31G. الوسيط |CitationClass= تم تجاهله (مساعدة)
  20. Bonanno, A.; Schlattl, H.; Paternò, L. (2002). "The age of the Sun and the relativistic corrections in the EOS". Astronomy and Astrophysics. 390 (3): 1115–1118. arXiv:astro-ph/0204331. Bibcode:2002A&A...390.1115B. doi:10.1051/0004-6361:20020749. الوسيط |CitationClass= تم تجاهله (مساعدة)
  21. Houdek, G.; Gough, D. (2011). "On the seismic age and heavy-element abundance of the Sun". Mon. Not. R. Ast. Soc. 418: 1217–1230. Bibcode:2011MNRAS.418.1217H. doi:10.1111/j.1365-2966.2011.19572.x. الوسيط |CitationClass= تم تجاهله (مساعدة)
    • بوابة علم الفلك
    في كومنز صور وملفات عن: علم الرجفات الشمسية
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.