طريقة هيون

الإجراء لحساب الحل العددي لمشكلة القيمة الأولية عن طريق تحسين طريقة يولر هو:

${\displaystyle y'(t)=f(t,y(t)),\qquad \qquad y(t_{0})=y_{0},}$

تحسين طريقة يولر عن طريق معادلة هيون على الشكل التالي:

${\displaystyle {\tilde {y}}_{i+1}=y_{i}+hf(t_{i},y_{i})}$

${\displaystyle y_{i+1}=y_{i}+{\frac {h}{2}}[f(t_{i},y_{i})+f(t_{i+1},{\tilde {y}}_{i+1})],}$

يتم استخدام طريقة يولر كأساس لطريقة هيون. تستخدم طريقة يولر خط التماس في بداية الفاصل الزمني كتقدير لمنحدر الدالة على الفاصل الزمني، على افتراض أنه إذا كان حجم الخطوة صغير، فسيكون الخطأ صغير. ومع ذلك، حتى عندما يتم استخدام أحجام خطوة صغيرة للغاية، على عدد كبير من الخطوات يبدأ الخطأ في التراكم ويختلف التقدير عن القيمة الفعلية. حيث يكون منحنى الحل مقعرا، فإن خط الظل الخاص به يقلل من الإحداثيات العمودية للنقطة التالية والعكس بالعكس لحل أسفل مقعر.[2]

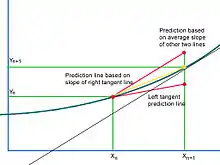
رسم بياني يوضح استخدام طريقة هيون لإيجاد تنبؤ أقل خطأ عند مقارنته بالترتيب الأدنى لطريقة يولر

${\displaystyle {\text{Slope}}_{\text{left}}=f(x_{i},y_{i})}$

${\displaystyle {\text{Slope}}_{\text{right}}=f(x_{i}+h,y_{i}+hf(x_{i},y_{i}))}$

${\displaystyle {\text{Slope}}_{\text{ideal}}=(1/2)({\text{Slope}}_{\text{left}}+{\text{Slope}}_{\text{right}})}$

وباستخدام مبدأ منحدر الخط = الارتفاع / المدى، يمكن العثور على الإحداثيات باستخدام الصيغة التالية:[3]

${\displaystyle {\text{Slope}}_{\text{ideal}}={\frac {\Delta y}{h}}}$

${\displaystyle \Delta y=h({\text{Slope}}_{\text{ideal}})}$

${\displaystyle x_{i+1}=x_{i}+h}$, ${\displaystyle \textstyle y_{i+1}=y_{i}+\Delta y}$

${\displaystyle y_{i+1}=y_{i}+h{\text{Slope}}_{\text{ideal}}}$

${\displaystyle y_{i+1}=y_{i}+{\frac {1}{2}}h({\text{Slope}}_{\text{left}}+{\text{Slope}}_{\text{right}})}$

${\displaystyle y_{i+1}=y_{i}+{\frac {h}{2}}(f(x_{i},y_{i})+f(x_{i}+h,y_{i}+hf(x_{i},y_{i})))}$

تحسين طريقة يولر على مرحلتين:

الطريقة الأولى:

الطريقة الثانية: وهي المشار إليها باسم طريقة هيون

يقلل هذا الأسلوب خطأ الاقتطاع.

• طريقة دورمند-برنس
• طريقة بوجاكي - شامبين
• طريقة باكورد يولر
• طرق غاوس-ليجندر

• بوابة رياضيات
• بوابة تحليل رياضي

في كومنز صور وملفات عن: طريقة هيون