شجرة AVL

في علم الحاسوب، شجرة إي في إل (بالإنجليزية: AVL Trees)‏ هي شجرة بحث ثنائية متزنة ، وهي أول بنية بيانات تم اختراعها.[1] في شجرة AVL، ارتفاع الأشجار الجزئية لأية عقدة تختلف بواحد على الأكثر. البحث، الإدخال، والحذف يتطلبون زمن (O(log n في كل من الحالات المتوسطة والأسوء، حيث أن n هو عدد العقد في شجرة قبل العملية. الإدخال والحذف قد يستلزم إعادة توازن الشجرة عن طريق دوران شجرة واحد أو أكثر.

مثال لشجرة AVL

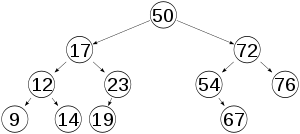
شجرة AVL سميت نسبة لمخرعيْها السوفيتيين، غيورغي ماكسيموفيتش أدلسن-فالسكي (Adelson-Velskii) ويفغيني لانديس (Landis). الذين نشراها في مقالهما سنة 1962 "خوارزمية لتنظيم المعلومات".[2]

عامل التوازن لعقدة ما هو ارتفاع الشجرة الجزئية اليسرى ناقص ارتفاع الشجرة الفرعية اليمنى (أحيانا العكس). والعقدة مع عامل توازن 1، 0 أو -1 تعتبر متوازنة. عقدة مع عامل توازن غير ذلك تعتبر غير متوازنة وتتطلب إعادة توازن الشجرة. عامل التوازن إما أن يكون محفوظا في كل عقدة، أو يتم حسابه من ارتفاعات أشجاره الجزئية.

عادة ما يتم مقارنة أشجار AVL مع أشجار أحمر-أسود لأنهما يدعمان نفس العمليات، ولأن أشجار أحمر-أسود يتطلبون زمن (O(log n في العمليات الأساسية. لأن أشجار AVL صارمون بالتوازن، هم أسرع من أشجار أحمر-أسود لتطبيقات المكثفة البحث.[3] من ناحية أخرى، أشجار أحمر-أسود هم أسرع بالإدخال والحذف.

عمليات

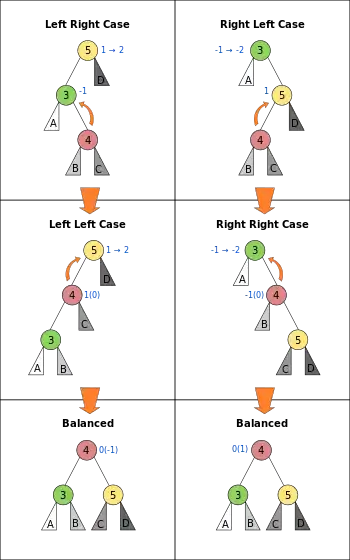
وصف مصور يظهر كيف أن عمليات دوران الشجرة تسبب إعادة توازن الشجرة. تمثل الأرقام العقد التي يتم موازنتها. المثلثات المعلمة بالحروف هي في حد ذاتها أشجار بحث ثنائية.

العمليات الأساسية في شجرة AVL تشتمل على تنفيذ نفس الأعمال الممكن تنفيذها على شجرة بحث ثنائية غير متوازنة، ولكن تسبق التعديلات أو تليها عملية واحدة أو أكثر تسمى دوران شجرة، والتي تساعد على استعادة توازن ارتفاع الأشجار الجزئية.

بحث

البحث في شجرة AVL يتم بالضبط مثل أية شجرة بحث ثنائية غير متوازنة. بسبب توازن ارتفاع الشجرة، يستغرق البحث زمن (O(log n، ولا يتم تعديل مبنى الشجرة في عملية البحث.

إذا كان لكل عقدة سجلات أحجام شجرتها الجزئية (شاملا العقدة نفسها وأحفادها)، إذن يمكن استعادة العقدة بزمن (O(log n أيضا.

حذف عقدة مع ابنين من شجرة بحث ثنائية

إدخال

بعد إدخال عقدة، لابد من التحقق من تمسك كل من أسلاف العقدة بقواعد AVL. لكل عقدة فحصت، إذا بقى عامل التوازن 1، 0 أو -1 إذن ليست هناك حاجة للدوران. من ناحية أخرى، إذا صار عامل التوازن ±2 إذن الشجرة الجزئية المبتدئة بهذه العقدة غير متوازنة. إذا تم الإدخال بشكل متسلسل، بعد كل إدخال، على الأكثر حالة واحدة من الحالات التالية يحب حلها لاستعادة قواعد AVL للشجرة كاملة.

هنالك أربع حالات يجب التطرق لها، بحيث أن حالتين متماثلتان للاثنتين الأخرى ين. ليكن P جذر شجرة جزئية غير متوازنة، مع L الابن الأيسر وR الابن الأيمن لـ P.

حالة يمين-يمين وحالة يمين-يسار:

إذا كان معامل توازن P هو -2 إذن يفوق ارتفاع الشجرة الجزئية اليمنى ارتفاع الشجرة الجزئية اليسرى، ويجب فحص معامل توازن الابن الأيمن (R). الدوران الأيسر مع P كالجذر ضروري.
إذا كان معامل توازن R هو -1، نحتاج دوران يساري واحد (مع P كالجذر) (حالة يمين-يمين).
إذا كان معامل توازن R هو +1، نحتاج دوارنين. الدوران الأول هو دوران يميني مع R كالجذر. الدوران الثاني هو دوران يساري مع P كالجذر (حالة يمين-يسار).

حالة يسار-يسار وحالة يسار-يمين:

إذا كان معامل توازن P هو +2 إذن يفوق ارتفاع الشجرة الجزئية اليسرى ارتفاع الشجرة الجزئية اليمنى، ويجب فحص معامل توازن الابن الأيسر (L). الدوران الأيمن مع P كالجذر ضروري.
إذا كان معامل توازن L هو +1، نحتاج دوران يميني واحد (مع P كالجذر) (حالة يسار-يسار).
إذا كان معامل توازن L هو -1، نحتاج دوارنين. الدوران الأول هو دوران يساري مع L كالجذر. الدوران الثاني هو دوران يميني مع P كالجذر (حالة يسار-يمين).

حذف

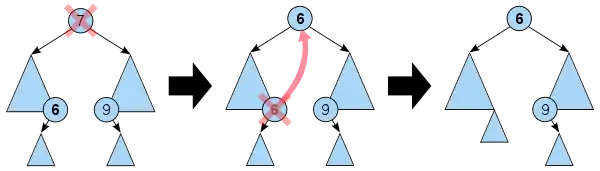
إذا كانت العقدة ورقة أو لها ابن واحد فقط، نزيلها. وإلا، نبدلها بإما الأكبر في الشجرة الجزئية اليسرى (السابق inorder predecessor) أو الأصغر في الشجرة الجزئية اليمنى (اللاحق inorder successor)، ونزيل العقدة.

مقارنة مع بنى بيانات أخرى

كلا من أشجار AVL وأشجار أحمر-أسود هم أشجار بحث ثنائية متوازنة ذاتيا، ولذلك هم متشابهون رياضيا. عمليتا إعادة التوازن الأشجار مختلفة، ولكن كلاهما يحدث في زمن (O(log n. الفرق الحقيقي بين الاثنتين هو تحديد الارتفاع. لشجرة بحجم $n$ :

ارتفاع شجرة AVL أقل بدقة من:[4]

\log _{\varphi }(n+2)-1={\log _{2}(n+2) \over \log _{2}(\varphi )}-1=\log _{\varphi }(2)\cdot \log _{2}(n+2)-1\approx 1.44\log _{2}(n+2)-1

بحيث أن $\varphi$ هو الرقم الذهبي. ارتفاع شجرة أحمر-أسود هو على الأغلب $2\log _{2}(n+1)$

إن أشجار AVL أكثر صرامة بالتوازن من أشجار أحمر-أسود، مما يؤدي إلى إدخال وحذف أبطئ ولكن استرجاع أسرع.

انظر أيضا

مراجع

Robert Sedgewick, Algorithms, Addison-Wesley, 1983, ISBN 0-201-06672-6, page 199, chapter 15: Balanced Trees.
Adelson-Velskii, G. (1962). "An algorithm for the organization of information". Proceedings of the USSR Academy of Sciences. 146: 263–266. الوسيط |CitationClass= تم تجاهله (مساعدة) (بالروسية) English translation by Myron J. Ricci in Soviet Math. Doklady, 3:1259–1263, 1962.
Pfaff, Ben (2004). "Performance Analysis of BSTs in System Software" (PDF). Stanford University. مؤرشف من الأصل (PDF) في 9 أغسطس 2017. الوسيط |CitationClass= تم تجاهله (مساعدة)
Burkhard, Walt (Spring 2010). "AVL Dictionary Data Type Implementation". Advanced Data Structures (PDF). La Jolla: A.S. Soft Reserves, UC San Diego. صفحة 99. مؤرشف من الأصل (PDF) في 26 أبريل 2020. اطلع عليه بتاريخ أغسطس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة); تحقق من التاريخ في: |تاريخ الوصول= (مساعدة); روابط خارجية في |ناشر= (مساعدة)

وصلات خارجية

exdgmime library by Dmitriy Vilkov: Straight C implementation could easily be taken from this library under GNU-LGPL and AFL v2.0 licenses.
Description from the Dictionary of Algorithms and Data Structures
Python Implementation
Single C header file by Ian Piumarta
AVL Tree Demonstration
AVL tree applet – all the operations
Fast and efficient implementation of AVL Trees
PHP Implementation

في كومنز صور وملفات عن: شجرة AVL

بوابة علم الحاسوب

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Robert Sedgewick, Algorithms, Addison-Wesley, 1983, ISBN 0-201-06672-6, page 199, chapter 15: Balanced Trees.

[2] Adelson-Velskii, G. (1962). "An algorithm for the organization of information". Proceedings of the USSR Academy of Sciences. 146: 263–266. الوسيط |CitationClass= تم تجاهله (مساعدة) (بالروسية) English translation by Myron J. Ricci in Soviet Math. Doklady, 3:1259–1263, 1962.

[3] Pfaff, Ben (2004). "Performance Analysis of BSTs in System Software" (PDF). Stanford University. مؤرشف من الأصل (PDF) في 9 أغسطس 2017. الوسيط |CitationClass= تم تجاهله (مساعدة)

[4] Burkhard, Walt (Spring 2010). "AVL Dictionary Data Type Implementation". Advanced Data Structures (PDF). La Jolla: A.S. Soft Reserves, UC San Diego. صفحة 99. مؤرشف من الأصل (PDF) في 26 أبريل 2020. اطلع عليه بتاريخ أغسطس 2020. الوسيط |CitationClass= تم تجاهله (مساعدة); تحقق من التاريخ في: |تاريخ الوصول= (مساعدة); روابط خارجية في |ناشر= (مساعدة)