خوارزمية هوبكروفت-كارب

هذه الخوارزمية تبحث عن الاقتران الأقصى في بيان ثنائي (G(U,V,E و هو الاقتران M ذو أكبر عدد ممكن من الحواف. هذه المشكلة NP-كاملة. خوارزمية هوبكروفت و كارب أول من حلت الاقتران الأقصى في وقت متعدد الأطراف.[1]

هذه مقالة غير مراجعة. ينبغي أن يزال هذا القالب بعد أن يراجعها محرر مغاير للذي أنشأها؛ إذا لزم الأمر فيجب أن توسم المقالة بقوالب الصيانة المناسبة. يمكن أيضاً تقديم طلب لمراجعة المقالة في الصفحة المُخصصة لذلك. (يونيو 2019)

إن هذه المشكلة تحظى باهتمام عملي كبير، تم طرحها في خمسينيات القرن العشرين وتبقى اليوم ذات أهمية كبيرة على سبيل المثال في ميدان التعلّم العميق وما يعرف بمشكلة تخصيص المهام في الأنظمة متعددة الروبوتات (أو أ سراب الروبوتات).

مصطلحات خوارزمية هوبكروفت كارب

رأس على حافة تنتمي إلى الإقتران M يقال رأس مشبع في M

رأس على حافة لا تنتمي إلى M يقال رأس حر بالنسبة إلى M

الاقتران الأقصى هو اقتران يحتوي على أكبر عدد ممكن من الحواف في (G(U,V,E

اقتران كامل في بيان ليس بالضرورة ثنائي متكون من 2N رأس، هو اقتران يتكون من N حواف
مسار M-متناوب في (G(U,V,E هو مسار تنتمي حوافه بالتناوب إلى اقتران (M ⊆ E(G و إلى المجموعته التكميلية E(G)-M

مسار M-متزايد هو مسار M-متناوب كلا طرفيه حران

يحتوي هذا المسار على حافة واحدة في E(G)-M إضافة إلى حواف M

الخوارزمية تعتمد على نظرية بيرج (1957)[2] الاقتران M هو الاقتران الأقصى إذا وفقط إذا كان (G(U,V,E لا يحتوي على مسار M-متزايد

خوارزمية هوبكروفت كارب (1973)

التهيئة M ← φ

علامة φ هنا تعني المجموعة الفارغة

طالما (G(U،V،E لديه مسار M متزايد P_i

ابحث عن أكبر مجموعة من أقصر المسارات M-متزايدة {P₁ ، P₂ ، ... ، P_max} التي تكون رؤوسها متمايزة

M ← M ⊖ P₁ ⊖ P₂ ⊖ ... ⊖ P_max

تهاية طالما

هنا العلانة ⊖ تدل على الفرق المتناظر أو الاختلاف الحصري للمجموعات

اِنغراز الإجراء الأساسي من أجل برمجة الخوارزمية

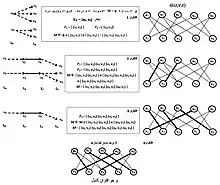
في كل خطوة أو تكرار، عملية البحث عن أكبر مجموعة من أقصر مسارات M_i-متزايدة بدون رؤوس مشتركة ترتكز على اقتران موجود M_i-1.

وجّه (G(U,V,E بحيث تكون حواف M في اتجاه v_i→u_i و حواف E(G)-M في الاتجاه المعاكس u_i → v_i. يصبح هكذا (G(U,V,E بيانا موجها غير حلقي
استخرج البيان الفرعي الذي تتوافق فيه الطرق الموجهة من رأس u_i حر إلى رأس v_i حر واحدة تلو الأخرى مع أقصر مسارات M-متزايدة، لذلك يجب :

تعليم البيان الفرعي حسب طبقات من الرؤوس ....، L₀ ،L₁ ، L₂ ، تنتمي الطبقات الزوجية إلى U ، والطبقات الفردية إلى V. تحتوي L₀ على رؤوس u_i حرة، المستوى الأخير L_t هو أدنى مستوى يحتوي على رؤوس v_i حرة

يجب إلغاء حواف u_i→v_j) E(G)-M) النازلة إلى مستوى أدنى

في الممارسة العملية، يمكن أن يؤدي تخصيص لخوارزمية BFS كل هذه الإجراءات في عملية موحدة في كل تكرار

مراجع

HOPCROFT, John E. et KARP, Richard M. An n^5/2 algorithm for maximum matchings in bipartite graphs. SIAM Journal on computing, 1973, vol. 2, no 4, p. 225-231.
BERGE, Claude. Two theorems in graph theory. Proceedings of the National Academy of Sciences of the United States of America, 1957, vol. 43, no 9, p. 842.

بوابة علم الحاسوب
بوابة خوارزميات

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] HOPCROFT, John E. et KARP, Richard M. An n^5/2 algorithm for maximum matchings in bipartite graphs. SIAM Journal on computing, 1973, vol. 2, no 4, p. 225-231.

[2] BERGE, Claude. Two theorems in graph theory. Proceedings of the National Academy of Sciences of the United States of America, 1957, vol. 43, no 9, p. 842.