انتقال دوراني
الانتقال الدوراني في الرياضيات لعناصر زمرة بحيث يصبح آخر عنصر مكان أول عنصر وتنقل جميع العناصر، أو يصبح العنصر الأول مكان العنصر الأخير وتنقل جميع العناصر.[1][2] بمعنى آخر النقل بشكل دوراني دون تغيير ترتيب العناصر التسلسلي ضمن الزمرة (عدا العنصر الأول والأخير). على سبيل المثال، الانتقال الدوراني لعناصر الزمرة (a, b, c) يعطي ما يلي:
- (a, b, c) (مطابقة للأصل)
- (c, a, b)
- (b, c, a)
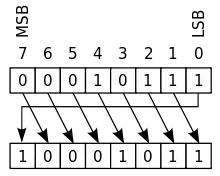
انتقال دوراني يميني بمقدار بت واحد
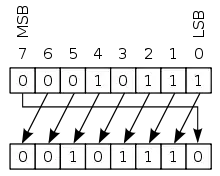
انتقال دوراني يساري بمقدار بت واحد
في علوم الحاسب، الانتقال الدوراني هو عملية تنقل بتات المعلومات بشكل مرتب دورانياً. على خلاف الانتقال الحسابي، فإن الانتقال الدوراني لا يحافظ على بت إشارة العدد أو يميز أس العدد من الفاصلة العشرية. وعلى خلاف الانتقال المنطقي، لا يتم ملئ البت الفارغ بالعدد صفر ولكن يملأ بالعدد الذي يأتي في ترتيب النقل. يستخدم الانتقال الدوراني عادة في تطبيقات علم التعمية لتقنية بسيطة لتشفير سلسلة من البتات.
مراجع
- Gruber, Hermann; Holzer, Markus (2009). "Language operations with regular expressions of polynomial size" (PDF). Theoretical Computer Science. 410 (35): 3281–3289. doi:10.1016/j.tcs.2009.04.009. Zbl = complete&q = an:1176.68105 1176.68105. مؤرشف من الأصل (PDF) في 29 أغسطس 2017. اطلع عليه بتاريخ أغسطس 2020. الوسيط
|CitationClass=تم تجاهله (مساعدة); تحقق من التاريخ في:|تاريخ الوصول=(مساعدة) - GCC: "Optimize common rotate constructs" نسخة محفوظة 03 مارس 2016 على موقع واي باك مشين.
- بوابة علم الحاسوب
- بوابة رياضيات
- بوابة تقنية المعلومات
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.