مستقيم قاطع

في الهندسة الرياضية، يطلق اسم المستقيم القاطع على المستقيم الذي يمر خلال مستقيمين أو أكثر يقعان في مستوي واحد عند نقاط مختلفة.[1][2][3]

ميّز عن خط قاطع.
المستقيم القاطع لمستقيمين متوازيين a وb

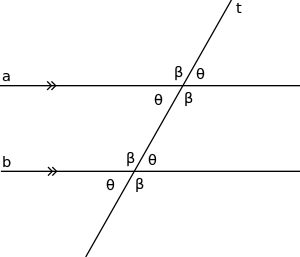
في الهندسة الإقليدية إذا كان المستقيمان a وb متوازيان وكان المستقيم t مستقيم قاطع لهما، فإن الزوايا التي تتشكل عند نقاط التقاطع تكون متطابقة. العلاقات بين المستقيمات والمستويات: التوازي والتخالف المستقيمان المتوازيان:مستقيمين لا يتقاطعان أبداً ويقعان في المستوى نفسه. المستقيمين المتخالفان:مستقيمين لا يتقاطعان ولا يقعان في المستوى نفسه. المستويان المتوازيان:مستويان غير متقاطعين. القاطع:المستقيم الذي يقطع مستقيمين أو أكثر في المستوى نفسه وفي نقاط مختلفه. علا قات أزواج الزوايا الناتجة عن القاطع : زوايا داخليه:زوايا تكون في المنطقة بين المستقيمين.مثل :الزوايا 3,4,5,6. زوايا خارجيه:زوايا ليست بين مستقيمين تكون في الأطراف.مثل:الزوايا 1,2,7,8. الزاويتين المتحالفتان:زاويتنا داخليتين واقعتان في جهة واحدة من القاطع.مثل:الزوايا4و5, 3و6. الزوايا المتبادله داخليا:زاويتان داخليتان غير متجاورتين تقعان في جهتين مختلفتين من القاطع .مثل الزوايا:3و5, 4و6. الزاويتين المتبادلتان خارجيا:زاويتان خارجيتان غير متجاورتين تقعان في جهتين مختلفتين من القاطع.مثل الزوايا:1و7, 2و8. الزاويتين المتناظرتان:هما زاويتان تقعان في جهة واحدة من القاطع وفي الجهة نفسها من المستقيمين.مثل الزوايا:1و5, 2و6 3و7, 4و8.

مراجع
  1. Rod Pierce (2011). "Parallel Lines". MathisFun. مؤرشف من الأصل في 17 يناير 2018. الوسيط |CitationClass= تم تجاهله (مساعدة)
  2. "Transversal". Math Open Reference. 2009. مؤرشف من الأصل في 16 أكتوبر 2017. الوسيط |CitationClass= تم تجاهله (مساعدة)
  3. C.Clapham, J.Nicholson (2009). "Oxford Concise Dictionary of Mathematics" (PDF). Addison-Wesley. صفحة 582. مؤرشف من الأصل (PDF) في 16 يونيو 2015. الوسيط |CitationClass= تم تجاهله (مساعدة)


    • بوابة رياضيات
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.