مخطط بياني خطي

المخطط البياني الخطي Line Chart أو المخطط الخطي هو أحد أنواع المخططات البيانية التي تعرض المعلومات كسلسلة من نقاط البيانات المتصلة بواسطة خطوط مستقيمة.[1] وهو النوع الأساسي من أنواع المخططات البيانية شائعة الاستخدام في كافة المجالات. ويتم إنشاء هذا المخطط بوصل سلسلة من النقاط التي تمثّل مقاييس مفردة بواسطة قطاعات خطية. غالباً ما يستخدم مخطط البيانات الخطي لعرض توجّه البيانات خلال فترات زمنية - أي أن الخط يُرسم زمنياً.[2]

يبين هذا المخطط البياني البسيط تغير البيانات عبر فترات زمنية مع نقاط متصلة

التركيب

يتم رسم المخطط البياني الخطي برسم خطين متعامدين يسميان "محورين". يسمى المحور الأفقي "محور السينات" ويسمى المحور العمودي "محور الصادات". للمساعدة في رسم المقاييس، يمكن أن يتم رسم المزيد من الخطوط المتوازية مع كل محور، وينتج عن ذلك ما يعرف بالشبكة. يمثل كل محور إحدى كميات البيانات التي سيتم رسمها. غالباً ما يستخدم محور الصادات العمودي لتمثيل المتغير التابع، ومحور السينات الأفقي (الإحداثي السيني) لتمثيل المتغير المستقل. ومن ثم يمكن القول أن المخطط يمثل "علاقة الكمية 1 مع الكمية 2"، بحيث يرسم الكمية 1 على المحور الصادي العمودي والكمية 2 على المحور السيني الأفقي.

تمثّل المحاور المفردة خطوط الأعداد وبذا فقد تتصمن علامات صغيرة تشير إلى القيم الهامة على الخط. هذا ويمكن وضع القيم على النقاط التي تمثلها. كما يتم وضع وصف قصير لكل محور. وقد يتم وصف المخطط البياني كاملاً بعنوان، وإذا تضمن المخطط أكثر من خط بياني واحد، فيضاف وصف لكل خط يسمى بالعنوان التفسيري أو المفتاح. أخيراً، ترسم البيانات عند تقاطعات الخطوط العمودية (الوهمية) الممتدة من المحاور، ومقاطع الخطوط المستقيمة التي يتم رسمها بين نقاط التقاطع.

مثال

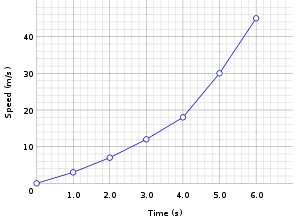
في العلوم التجريبية، يتم رسم البيانات التي تجمع من التجارب في مخططات بيانية. على سبيل المثال، إذا جمع أحدهم معلومات عن سرعة الجسم عند فترات زمنية معينة، فإن بإمكانها تمثيل تلك البيانات في جدول بيانات كما يلي:

مخطط بياني يمثل تغيّر السرعة عبر الزمن
الزمن المقطوع السرعة (متر)
0 0
1 3
2 7
3 12
4 20
5 30
6 45

إن تمثيل الجدول بيانياً هو طريقة رائعة لعرض القيم بالضبط، لكنها في ذات الوقت طريقة ضعيفة لفهم الأنماط التي تمثلها تلك القيم. يتم تسهيل فهم العملية التي تصفها البيانات المنظمة في الجدول بواسطة المخطط البياني الخطي "السرعة مقابل الوقت". ويوضح الشكل في الطرف الأيسر هذا المخطط. رياضياً، إذا عبّرنا عن الزمن بالمتغير الرياضي "ز"، والسرعة بالمتغير الرياضي "ع"، فإنه يمكن التعبير عن العلاقة المرسومة في المخطط بالاقتران "ع(ز)"، ما يعني أن المتغير التابع "ع" هو اقتران لـ "ز".

أفضل مطابقة

غالباً ما تتضمن المخططات البيانية اقتراناً رياضياً (دالة رياضية) تمثل اتجاه "أفضل مطابقة" للبيانات الموزعة. وتسمى هذه الطبقة بطبقة أفضل مطابقة ويسمى المخطط البياني الذي يتضمن تلك الطبقة بالمخطط البياني الخطي. من السهل رسم "طبقة أفضل مطابقة" تحتوي على مجموعة من القطاعات الخطية التي تصل بين نقاط البيانات المتجاورة.

  • ليس من الوارد أن الانقطاعات في منحنى "أفضل مطابقة" تنطبق تماماً مع مواقع القيم المقاسة.
  • من غير المحتمل أن يكون الخطأ التجريبي في البيانات مهملاً، ومع ذلك فإن المنحنى يقطع كل نقطة من نقاط البيانات.

في الحالتين، يمكن أن تكشف طبقة "أفضل مطابقة" اتجاهات البيانات. يمكن أن تمثّل القياسات أو المساحة المحصورة تحت المنحنى، ما يؤدي إلى الحصول على المزيد من الاستنتاجات أو النتائج من البيانات.

يجب أن تمثل طبقة أفضل مطابقة الفعلية اقتراناً (دالة) رياضياً مستمراً بحيث تحدد مَعْلماته باستخدام نمط ملائم للتقليل من الخطأ. قد تتغيّر منحنيات أفضل مطابقة من البسيط، كما في المعادلات الخطية إلى المعقد، كما في المنحنيات التربيعية واقترانات كثيرة الحدود والاقترانات الأسية والدورية.[3] والمنحنى جرسيّ الشكل أو التوزيع الطبيعي الذي يستخدم عادة في الإحصاء هو عبارة عن اقتران غاوس.

طالع أيضاً
في كومنز صور وملفات عن: مخطط بياني خطي

المراجع
  1. Burton G. Andreas (1965). Experimental psychology. p.186
  2. Neil J. Salkind (2006). Statistics for People who (think They) Hate Statistics: The Excel Edition. page 106.
  3. "Curve fitting". The Physics Hypertextbook. مؤرشف من الأصل في 23 مارس 2019. الوسيط |CitationClass= تم تجاهله (مساعدة)
    • بوابة إحصاء
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.