مبرهنة يابانية في مضلع دائري

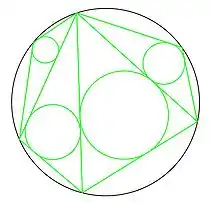
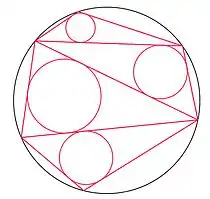
في الهندسة الرياضية، تنص المبرهنة اليابانية على أنه مهما كان شكل تثليث مضلع دائري، فإن مجموع أنصاف أقطار الدوائر الداخلية للمثلثات يكون ثابتا.[1][2][3]

مجموع أنصاف أقطار الدوائر الخضراء = مجموع أنصاف أقطار الدوائر الحمراء

وعكس المبرهنة أيضاً صحيح، بحيث إذا كان مجموع أنصاف أقطار الدوائر الداخلية لتثليث معين مستقلاً عن شكل التثليث، فإن المضلع يكون دائرياً.

مراجع
  1. Fukagawa, Hidetoshi; Pedoe, D. (1989). Japanese Temple Geometry. Manitoba, Canada: Charles Babbage Research Center. صفحات 125–128. ISBN 0919611214. الوسيط |CitationClass= تم تجاهله (مساعدة)
  2. In search of "Japanese theorem نسخة محفوظة 29 يوليو 2010 على موقع واي باك مشين.
  3. Reyes, Wilfred (2002). "An Application of Thébault's Theorem" (PDF). Forum Geometricorum. 2: 183–185. مؤرشف من الأصل (PDF) في 24 أكتوبر 2018. اطلع عليه بتاريخ 02 سبتمبر 2015. الوسيط |CitationClass= تم تجاهله (مساعدة)
    • بوابة رياضيات
    • بوابة هندسة رياضية
    مبرهنة يابانية في مضلع دائري في المشاريع الشقيقة
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.