مبرهنة مورلي

في الهندسة الرياضية، تنص مبرهنة مورلي على أنه في أي مثلث، إن قاسمات الزوايا إلى ثلاث زوايا طبوقة تتقاطع في ثلاث نقاط مشكلة مثلث متساوي الأضلاع يسمى مثلث مورلي.[1][2][3] تم اكتشاف هذه المبرهنة في عام 1899 من قبل الرياضياتي الأمريكي فرانك مورلي.

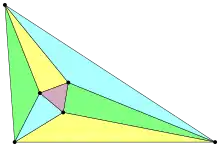
مثلث مورلي

تأخذ المبرهنة اهتماماً خاصة لعدم وجود طريقة في الهندسة الإقليدية لإنشاء قاسم ثلاثي لزاوية (تثليث زاوية)، وبالتالي عدم وجود طريقة لإنشاء مثلث مورلي المتساوي الأضلاع.

مراجع

Clifford, Pickover (2010). Le Beau Livre des Maths. Dunod. ISBN 978-2-10-054640-4. 296 الوسيط |CitationClass= تم تجاهله (مساعدة)
J. Conway's proof, from Bogomolny. نسخة محفوظة 10 يوليو 2018 على موقع واي باك مشين.
Ces problèmes qui font les mathématiques (la trisection de l'angle), Publication de l'A.P.M.E.P., n^o 70, 1988, ص. 54 . نسخة محفوظة 04 مارس 2016 على موقع واي باك مشين.

بوابة رياضيات
بوابة هندسة رياضية

في كومنز صور وملفات عن: مبرهنة مورلي

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[1] Clifford, Pickover (2010). Le Beau Livre des Maths. Dunod. ISBN 978-2-10-054640-4. 296 الوسيط |CitationClass= تم تجاهله (مساعدة)

[2] J. Conway's proof, from Bogomolny. نسخة محفوظة 10 يوليو 2018 على موقع واي باك مشين.

[3] Ces problèmes qui font les mathématiques (la trisection de l'angle), Publication de l'A.P.M.E.P., n^o 70, 1988, ص. 54 . نسخة محفوظة 04 مارس 2016 على موقع واي باك مشين.