طرق حساب الجذر التربيعي
في التحليل العددي، هناك عدة طرق لحساب الجذر التربيعي الرئيسي (أي الموجب) لعدد حقيقي موجب. عادة ما تعطي هذه الطرق قيمة مقربة للجذر التربيعي المراد حسابه.
الطريقة البابلية
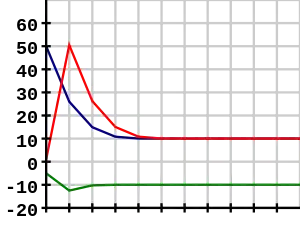
Graph charting the use of the Babylonian method for approximating the square root of 100 (10) using starting values
x0 = 50,
x0 = 1,
and x0 = −5. Note that using a negative starting value yields the negative root.
انظر إلى هيرو السكندري وإلى طريقة نيوتن.
أولا : نختار قيمة للعدد (من الأحسن إختاره حيث بالقريب إلى الوحدة حيث S هو العدد الذي نريد حساب جذره التربيعي)
ثانيا : نحسب الأعداد الحدود المتتالية للمتتالية و نتوقف عند العدد حيث
أمثلة
لحساب , حيث S = 125348,
هكذا,
لحساب , حيث S = 27,
هكذا,
طريقة القيمتين الدنيا والقصوى
انظر إلى طريقة التنصيف.
التمثيل العشري
تمكن من حساب قيمة تقريبية لجذر مربع عدد ما.
- يقسم العدد من اليمين إلى اليسار، إلى زمر من رقمين:مثلا 11878 يصبح 78 18 1.
- نبحث عن الجذر القريب للزمرة الأولى أقصى اليسار:هنا 1 والجذر هو 1.
- نحسب الباقي الزمرة ناقص مربع العدد:هنا نجد 0.
- ننزل الزمرة الموالية إلى جانب الباقي:هنا نحصل على 18 أي 018
- نضاعف الجذر الجزئي المحصل عليه حاليا:هنا 2.
- نحدف رقم الوحدات للعدد المحصل عليه في 4:نحصل على 1.
- نقسم العدد المحصل عليه في 6، على العدد المحصل عليه في 5، والعدد المحصل عليه سيكون هو الرقم الموالي للجذر:هنا 1 على 2 تساوي 0.
- نضع الرقم المحصل عليه في 7 على يمين العدد المحصل عليه في 5:هنا نجد 20
- نضرب العدد المحصل عليه في 8، في العدد المحصل عليه في 7:هنا نجد 20 في 0 يساوي 0.
- نطرح من العدد المحصل عليه في 4، العدد المحصل عليه في 9:هنا نجد 18 وفي حالة الحصول على عدد سالب نطرح واحد من العدد المحصل عليه في 7 ونستأنف العملية.
- ننزل الزمرة الموالية إلى جانب الباقي المحصل عليه في 10:هنا نجد 1878
- نعيد العمليات انطلاقا من المرحلة 5.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.