شعاع الدعم الآلي

تندرج آلات المتجهات الداعمة (أو شبكات المتجهات الداعمة) تحت خوارزمات تعلم الآلة المراقبة (المرمزة) لتحليل البيانات من أجل تصنيفها تصنيفًا إحصائيًا وعمل تحليل الإنحدار اللازم لها. يكون المدخل للعملية هي جزء من البيانات من أجل مران الخوارزم وتكون مرمزة بتصنيفها لإحدى الفصيلتين؛ منتمية للنوعية س أو لا منتمية لها.عندما ترسم البيانات على محاور الخصائص، يقوم الخوارزم بإيجاد إطار خطى للفصل بين خصائص كلٍ من النوعيتين بحيث تكون الهوة بينهما متسعة قدر ما يمكن. ثم تتم عملية التعلم نفسها عقب المران حيث يتم تصنيف جزء آخر من البيانات تبعًا للإطار الذي وُجد في عملية المران. إلى جانب قدرة خوارزم الدعم الآلى على إيجاد الإطار الخطي، تتمكن أيضًا من إيجاد أُطر غير خطية بتطبيق خدعة المصفوفة

تعد من أشهر طرق التصنيف الأتوماتيكي لتعلم الآلة، تعتمد على إيجاد منحني أو مستوي فائق يفصل العينات المدخلة عن بعضها البعض، ويتميز بإستخدامه في تصنيف المسائل ذات الفئات الثنائية: 1 للعينات الإيجابية أو -1 للعينات السلبية. على سبيل المثال: لتصنيف عينات بيانات مرضى تخص مرض الإيدز، إذا كان المخرج 1 يعني أن الشخص مصاب بمرض الإيدز، وإذا كان المخرج -1 يعني أن الشخص غير مصاب بمرض الإيدز.[1][2]

التعريف

تقوم هذه الخوارزمية بحساب سطح أو مجموعة أسطح في بعد آخر يختلف طوله عن طول متجه الخصائص. تحدد دقة الخوارزمية بقدرتها على الفصل بين الفئتين بحيث تكون أقرب عينة من كلى الفئتين أبعد ما يكون عن بعضهما البعض وهو ما يسمى بالحافة، وبصفة عامة كلما زادت الحافة أو هامش الفصل، كلما قل الخطأ في حالة التعميم لجزء البيانات الغير خاص بمرحلة المران. بالرغم مما تبدو عليه المشكلة من سهولة، إلا أنه في أغلب الأحيان لا يمكن الفصل بين الفئتين خطياً، وحينها نلجأ لتحويل محاور متجهات الخصائص لبعد أعلى بحيث يتم الفصل بينهم بسطح. ويراعى في هذا المنظور العبء الحسابى فيتم حساب الضرب القياسى للمتجهات بواسطة دالة المصفوفة، حيث يكون السطح الفاصل معرف بمجموعة من النقاط نتاج ضربهم القياسى مع متجه في الإحداثيات الجديدة (ذات البعد الأعلى) تكون ثابتة.

التاريخ

في عام 1963، اخترع العالمان فلاديمير فابنك وأليكسى شيرفونينكيز خوارزمية آلات المتجهات الداعمة. أما الخوارزمية المستخدمة حاليا (الهامش المرن) فقد طرحها كورينا كورتز وفابنك على 1993 ونُشرت عام 1995.

الأهمية

إن عملية تصنيف البيانات تعد من أكثر عمليات تعلم الآلة شيوعاً. بوجود نقاط البيانات التي تنتمى لفئة من اثنين، يكون الهدف هو تصنيف نقطة جديدة وتحديد لأىٍ من الفئتين تنتمى. ينظر لنقطة البيان على أنها متجه له عدد ج من الخصائص، وإذا تم الفصل بسطح بُعده ينقص عن ج بواحد يكون التصنيف خطياَ، ويكون غير خطيا ما عدا ذلك. وفي حالة توافر أكثر من فاصل خطى، يتم اختيار الفاصل الذي يضمن هامش أوسع بين أقرب نقطتين من نوعيتين مختلفتين وهو ما يسمى بالمستوى ذو الهامش الأكبر.

طریقة عمل آلات المتجهات الداعمة الخطية

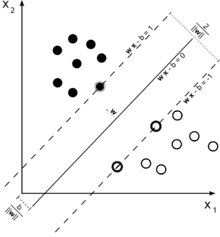
تكون المعطيات مجموعة من النقاط س عددها ن ويكون متجه خصائصها طوله ج والمتجه ص بطول ن و كل قيمة فيه تكون إما واحد (منتمية للفئة المعنية) أو سالب واحد (غير منتمية لها). كل متجه س ك يكون طوله ص حيث تتراوح قيمة ك بين 1 ون. يكمن هدف خوارزم في إيجاد المستوى الذي يفصل بين الفصيلتين (المرمزة 1 وعكسها وتكون مرمزة 1-) مع وجود أكبر وأوسع هامش بين الفصيلتين. العينات من البيانات التي تقع على هذا الهامش تسمى بمتجهات الدعم التي تحقق المعادلة
س . ف – ب =0 و تمثل علامة النقطة (.) الضرب القياسى للمتجهات، ويمثل ب/‖ف‖ مقدر إزاحة المستوى الفاصل عن نقطة الأصل باتجاه المتجه ف العمودى على هذا المستوى. أما مقدار الهامش فيكون 2/‖ف‖ ويهدف الخوارزم لتقليل المتجه ف بحيث تزيد قيمة هامش (حافة)الفصل.
تخضع العينات الإيجابية (المنتمية للنوعية) للمعادلة س . ف – ب ≥ 1، أما العينات السلبية فتخضع للمعادلة س . ف – ب ≤ 1-.
و بإعادة تنسيق المعادلات نصل إلى مشكلة الأمثلة
و تصبح إيجاد أقل‖ف‖^2/2 خاضعة لشرط

ص ك (س ك . ف – ب) ≥ 1 لكل قيم ك ما بين 1 ون.[3]

شعاع الدعم الآلي يفصل بين عينات من فئتين

طریقة عمل آلات المتجهات الداعمة اللاخطية

في عام 1992 اقترح برنارد بوسر، ايزابيل جيون، وفلاديمير فابنك طريقة لخلق خوارزمية التصنيف غير الخطى بتطبيق خدعة المصفوفة (المُقتَر من قِبَل إيزارمان وآخرون). الخوارزمية النهائية تكون شبيه بالخطى مع استبدال كل عملية ضرب قياسى بمصفوفة لا خطية، وبذلك تقوم الخوارزمية بإيجاد المستوى ذو الهامش الأقصى في إحداثيات الخصائص بعد تحويلها. و من أشهر تلك المصفوفات:
- متعددة الحدود المتجانسة : ع (س ك، س ل) = (س ك . س ل )^ز
- متعددة الحدود الغير متجانسة: ع (س ك، س ل) = (س ك . س ل +1 )^ز
- دالة جاوس المعتمدة قيمتها على البعد من نقطة الأصل: ع (س ك، س ل) =ه(-γ || س ك- س ل ||^2) ، حيث تكون γ > 0 حيث ع هي دالة المصفوفة

آلات المتجهات الداعمة الخطية ذات الهامش المرن

في عام 1995، اقترح كورينا كورتز وفلاديمير فابنك خوارزمية معدِلة لفكرة الهامش الأقصى مع السماح بوجود عينات يتم ترميزها برمز خاطئ. إذا تعذر وجود مستوى يفصل بين العينات الموجبة والسالبة، تقوم فكرة الهامش المرن على إيجاد مستوى يفصل بين نوعى العينتين بأقل خطأ ممكن بحيث تتواجد (تُرمز) أقل عدد من العينات برمز خاطئ. و تصبح مشكلة الأمثلة هي إيجاد
أقل ‖ف‖^2/2 + دك∑ * ط لكل قيم ك ما بين 1 ون
و تكون خاضعة ً لشرط ص ك (س ك . ف – ب) ≥ 1- دك لكل قيم ك ما بين 1 ون، حيث تحدد المتغيرات دك الغير سالبة درجة خطأ التمييز للعينة س ك.[4]

انظر أيضًا

المراجع

[ما هي؟]

  1. [1] H. Byun and S.-W. Lee, "Applications of support vector machines for pattern recognition: A survey," in Pattern recognition with support vector machines, ed: Springer, 2002, pp. 213-236.
  2. [1] C. Cortes and V. Vapnik, "Support-vector networks," Machine learning, vol. 20, pp. 273-297, 1995.
  3. Gino J. Lim and Eva K. Lee (2008). Optimization in Medicine and Biology. New York: Auerbach Publications. ISBN 9780849305634
  4. Richard O. Duda, Peter E. Hart, and David G. Stork (2000). Pattern Classification (2nd ed.). ISBN 0471056693

    وصلات خارج ويكي

    An Idiot’s guide to Support vector machines SVMs

    svmtutorial.pdf

    من أشهر المكتبات التطبيقة لشعاع الدعم الآلي، تضم تطبيقات في العديد من لغات البرمجة libsvm

    • بوابة إحصاء
    • بوابة علم الحاسوب
    • بوابة تقنية المعلومات
    This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.