زاوية أقصى انحدار

زاوية أفصى انحدار (أو استلقاء) لمستوى α (ألفا) هي الزاوية الزوجية بين ألفا ومستوى أفقي مرجعي π. لقياس هذه الزاوية يمكن أن يتم بقطع المستويين الفا وبي بمستوى ثالث γ (غاما) بحيث يكون عمودي على α π، الزاوية التي تتكون بين الخطوط الناتجة عن تقاطع تلك المستويات (γ مع α وγ مع π) هي الزاوية المطلوبة, أي زاوية أفصى انحدار للمستوى α.

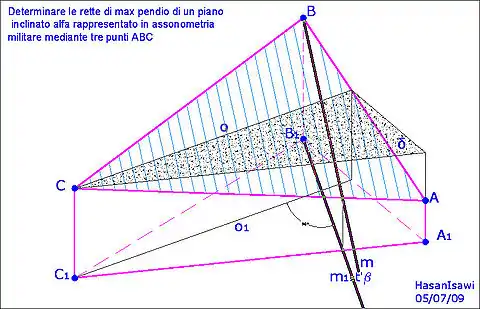
يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوقة. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (مارس 2016)
شكل 1: تحديد خطوط أقصى انحدار لسطح مائل ممثل في الإسقاط الاكسنومتري عن طريق ثلاثة نقط. زاوية أقصى انحدار للمستوى ABC, في الشكل المرفق, هي المكونة بين الخطين m و m1

مثال (شكل 1)
  • قُرر أن لدينا الإسقاط الاكسونومتري لمستوى الفا محدد من خلال 3 نقط ABC (انظر الشكل 1) ويُرغب في تحديد اتجاهات خطوط أقصى انحدار لذلك المستوى بحيث تكون متباعدة بينها بمسافة تساوي س.

الإجراء

يُعرف أن خطوط أقصى انحدار لمستوى ألفا يجب أن تكون عمودية على الخطوط الأفقية التي تنتمي لنفس المستوى ألفا. لإيجاد خط افقي o, يُقطع ألفا بمستوى أفقي دلتا. حالما نجد o, وبما ان الصورة الاكسونومترية للزاوية بين خط أقصى انحدار m والخط الأفقي o ليست حقيقية، يُشرع بإسقاط o على المستوى الأفقي بي لإيجاد المسقط الأول o1 للخط الأفقي o. ثم يرسم الإسقاط الأول m1 (لخط أقصى انحدار m) بطريقة متعامدة على o1. بعد أن نجد m1, نسقطه على ألفا باستخدام مستوى رأسي بيتا. وبهذا يحدد خط أقصى انحدار m للمستوى ألفا كخط تقاطع بين المستويين الفا وبيتا. الخطوط الأخرى الأقصى انحدار للمستوى ألفا ستكون موازية للخط m. لتحديد المسافة بين هذة الخطوط، نُعين, انطلاقاً من النقطة C، نقط تبعد عن بعضها بمسافة تساوي المقياس المعطى x, ومن هذه النقط ترسم تلك الخطوط بحيث تكون موازية للخط m. وهذا ما هو مطلوب.

انظر أيضاً

وصلات خارجية
  • بوابة رياضيات
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.