رياضيات التذبذب

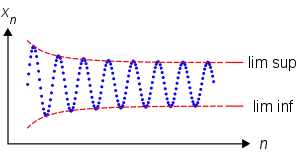
السماح يكون تسلسل من الأرقام الحقيقية. التذبذب من هذا التسلسل هو الذي يعرف بأنه الفرق (ربما لا حصر له) بين الحد الأعلى و الحد أدنى من :

${\displaystyle \omega (a_{n})=\limsup _{n\to \infty }a_{n}-\liminf _{n\to \infty }a_{n}}$.

التذبذب هو الصفر إذا و فقط إذا كان تسلسل يتقاطع. هو غير معروف إذا و كلاهما يساوي +∞ أو كليهما يساوي −∞, وهذا هو, إذا كان تسلسل يميل إلى +∞ أو −∞.

السماح تكون قيمتها الحقيقية وظائف حقيقية متغير. التذبذب على فاصل في المجال هو الفرق بين supremum و infimum من :

عموما ، إذا دالة على طوبولوجي الفضاء (مثل متري الفضاء) ، ثم التذبذب على فتح مجموعة هو

${\displaystyle \omega _{f}(U)=\sup _{x\in U}f(x)-\inf _{x\in U}f(x).}$

التذبذب وظيفة حقيقية متغير في نقطة يتم تعريف الحد من التذبذب على -حي :

${\displaystyle \omega _{f}(x_{0})=\lim _{\epsilon \to 0}\omega _{f}(x_{0}-\epsilon ,x_{0}+\epsilon ).}$

هذا هو نفس الفرق بين الحد الأعلى و الحد أدنى وظيفة في , توفير نقطة ليس مستبعدا من الحدود.

عموما ، إذا هو قيمتها الحقيقية الدالة على الفضاء المتري ، ثم التذبذب هو

${\displaystyle \omega _{f}(x_{0})=\lim _{\epsilon \to 0}\omega _{f}(B_{\epsilon }(x_{0})).}$