رسم ثلاثي الأبعاد
الرسم ثلاثي الأبعاد هو رسم المجسمات الحقيقية الموجودة في الطبيعة مع تبيين أبعادها الثلاثة. وللرسم ثلاثي الأبعاد عدة طرق للرسم، مشهورة وغير مشهورة، أما أشهرها فهي طريقة الرسم بزاوية 45 درجة، وهناك أيضاً: طريقة الرسم بزاوية 30 درجة، ولكل منها خصائصه التي تميزها عن غيرها.
يفتقر محتوى هذه المقالة إلى الاستشهاد بمصادر. فضلاً، ساهم في تطوير هذه المقالة من خلال إضافة مصادر موثوقة. أي معلومات غير موثقة يمكن التشكيك بها وإزالتها. (مارس 2016)
طرق الرسم ثلاثي الأبعاد
تبين هذه المقالة بعض الطرق للرسم ثلاثي الأبعاد وذكر مزاياها، وهذه الطرق هي: الرسم بزاوية 45° والرسم بزاوية 30°
بعض المصطلحات المهمة قبل بداية الرسم
من المهم جداً التعرف على بعض المصطلحات قبل تعلم كيفية الرسم ثلاثي الأبعاد:
النقطة: وهي كائن عديم الأبعاد، لا طول له ولا مساحة ولا حجم، وإنما لها موقع فقط.
الخط المستقيم: هو الكائن الواقع في بعد واحد ويملك طولاً محدداً ولا مساحة له ولا حجم، ويتحدد بنقطتين على الأقل.
المستوي: هو سطح في الفراغ يتواجد في بعدين اثنين، يملك طولاً وعرضاً, وبالتالي مساحةً, يتحدد بثلاث نقاط ليست على استقامة واحدة على الأقل، ومثاله المربع.
المجسم: كائن يحتل ثلاثة أبعاد، له طول وعرض وارتفاع، وله مساحة وحجم، يتحدد بأربع نقاط ليست في مستو واحد على الأقل.ومثاله المكعب.
الزاوية: مقياس لميل مستقيمين أحدهما على الآخر، يلتقيان في نقطة ما.
والآن، بمعرفتك للأمور السابقة، لنبدأ بتعلم طريقتي الرسم المشهورتين، والمبسطتين (الرسم بزاوية 45° والرسم بزاوية 30°)
ثم ننتقل إلى طريقة متقدمة في الرسم، وهي طريقة تناسب الأبعاد الثلاثة مع بعدين اثنين, طريقة وجدتها للرسم ثلاثي الأبعاد، لا أستطيع ادعاء ابتكارها, ,وإنما جلّ ما فعلته هو وضع القواعد لها، ولما لم أجد لها اسماً, سميتها بالاسم المذكور آنفاً, أرجو أن أوفق في شرحها، وما يميزها عن طرق الرسم الأخرى أنها تعطي الشكل الحقيقي كما تراه عينك على أرض الواقع.
طريقتا الرسم المشهورتان
قبل البدء، يجب أن تعلم أن طرق الرسم السابقة، لها فوائد عديدة، أهمها تبسيط طريقة الرسم. ويفيد قارئ الرسمة كثيراً أن يعلم بأي طريقة رسمت الرسمة، ولكن الرسومات التي نرسمها بهذه الطريقة ليست الصور الحقيقة للمجسم، وإنما صورة توضيحية لأبعاد المجسم.
الرسم بزاوية 45°
لنبدأ بالطريقة الأولى: الرسم بزاوية 45°: وهي رسم الجسم ثلاثي الأبعاد بحيث يكون البعد الثالث له مائلاً بزاوية 45° في مستوى صفحة الرسم، لنطبق ذلك على جسم بسيط، وليكن المكعب:
المعلومات المطلوبة: نريد رسم مكعب طول ضلعه 7 وحدات (عند تطبيقك للدرس أقترح أن تختار الوحدة كما تشاء، ولتكن "سنتمتراً" , وبالتالي يكون طول ضلع المكعب عندك 7 سم).
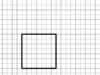
1- نرسم المسقط الأمامي (وجه المكعب) على شكل مربع طول ضلعه 7 وحدات.
ثم
2- نرسم امتداداً بزاوية 45 درجة من كل زاوية من زوايا المربع، لاحظ أنني رسمت الخط الخارج من الزاوية السفلى اليسرى على شكل خط مقطع، وذلك لأنه لن يظهر في رسمة النهائية.
ثم
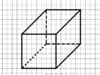
3- نصل بين هذه الخطوط مراعين الخطوط التي لن تظهر نرسمها بشكل متقطع.
وأخيراً
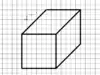
4- نمحو الخطوط التي لا تظهر في الشكل النهائي (وهي الخطوط المقطعة), فنصل للرسمة النهائية.
هذه هي الطريقة بكل بساطة، يمكنك تطبيقها على أي شكل، مراعياً أن يكون أي امتداد ترسمه (الذي يتجه في الواقع لداخل الصفحة)مائلاً بزاوية 45°
الرسم بزاوية 30°
الطريقة الثانية: الرسم بزاوية 30°:
وهي رسم الجسم ثلاثي الأبعاد بحيث يكون البعد الثالث له مائلاً بزاوية 30° في مستوى صفحة الرسم، لنطبق ذلك على المكعب أيضاً:
المعلومات المطلوبة: نريد رسم مكعب طول ضلعه 7 وحدات (أقترح 7سم على ورقة الرسم)
1- نرسم المسقط الأمامي (وجه المكعب) على شكل مربع طول ضلعه 7 وحدات
ثم
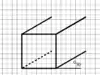
2- نرسم امتداداً بزاوية 30° من كل زاوية من زوايا المربع
ثم
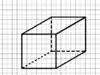
3- نصل بين هذه الخطوط مراعين الخطوط التي لن تظهر نرسمها بشكل متقطع
وأخيراً
4- نمحو الخطوط التي لا تظهر في الشكل النهائي (وهي الخطوط المقطعة), فنصل للرسمة النهائية
كما يمكن تطبيق هذه الطريقة بكل بساطة على أي شكل مجسم ثلاثي الأبعاد، مراعياً الخط الذي يتجه في الواقع داخل الصفحة أن يميل بزاوية 30°
تناسب الأبعاد الثلاثة مع بعدين اثنين
نأتي الآن إلى طريقة الرسم الثالثة
وضحت سابقاً أن طرق الرسم السابقة إنما لتوضيح أبعاد المجسم لنر كيف يمكن رسم صورة ثلاثية الأبعاد كما تظهر أمام عين المشاهد.
رسم الخط المائل بمركباته
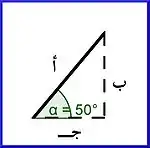
لنأخذ كبداية: طريقة مبسطة لرسم أي خط مائل في البعدين بدلالة خطين متعامدين
وهي أن ترسم الخط المائل بزاوية α مع محور السينات الموجب بحيث تستخدم المسطرة في رسم خطين متعامدين أحدهما مواز لمحور السينات والآخر للصادات … وبالتالي يكون طول الموازي للسينات يساوي طول الضلع المراد رسمه مضروباً في (جتا α) والموازي للصادات طوله يساوي طول الضلع المراد مضروباً في جاα ففي الرسمة المجاورة لرسم أ والذي نريد طوله =10 وحدات نرسم ب وطوله =10*جا50° و ج وطوله = 10*جتا50°
ولكن ماذا عن الخط الذي يكون في البعد الثالث (ملاحظة الخط دائماً في بعد واحد ولكن القصد أن له علاقة مع المحاور الأساسية الثلاث-كأن يكون في مجسم)؟
هنا تكمن أهمية هذه المعلومة ؛حيث إننا في كل الرسومات نريد أن نحول الرسمة التي نرسمها من ثلاثية الأبعاد إلى ثنائية الأبعاد (مستوى صفحة الرسم)
رسم الخط المتجه أصلاً داخل الصفحة
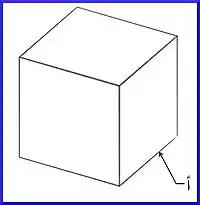
ولنطبق ذلك على المكعب، فنبدأ به خطاً خطاً
ولكن قبل ذلك علينا أن نعرف كم درجة مال كل خط في المحاور التي دار فيها ولذلك نوضح الرسمة كالتالي
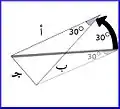
أولاً: المكعب دار بزاوية 30° مع عقارب الساعة عند النظر إليه من الأعلى و 30° بعكس عقارب الساعة عند النظر إليه من الجانب الأيمن كما في الصورة
في الصورة التالية تبيين لطريقة دوران المكعب، لأتأكد أنك استوعبت طريقة التدوير 100% - كما يمكن العودة إليها متى احتجت في وقت لاحق من قرائتك للموضوع:
بعد أن علمنا كيف دار المكعب، نريد أن نحدد الهدف وهو : رسم المكعب كما سيظهر من المسقط الأمامي بعد الدوران
ولنبدأ برسم الخط أ – والذي كان قبل الدوران داخل الصفحة
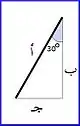
لنتتبع دوران الخط أ :نتخيل وكأن الخط عندما دار في
المرة الأولى تحول إلى خط ذو مركبتين متعامدتين , سينية وصادية بمعنى أننا لو رسمنا هاتين المركبتين ثم وصلنا بين بداية المركبة السينية ونهاية الصادية نحصل على الخط المطلوب بعد (دورة 1) –أي كما تم الشرح في الأعلى- ... أي أننا نستطيع رسم المركبتين فقط والاستغناء عن الخط الأصلي، وهذا ما سيحدث
نريد أن ننظر إلى الخط أ وحده من الأعلى : قبل الدوران كان كما في الصورة التالية:
ثم أصبح كالتالي (سنسمي الخطوط الوهمية بـ ب، ج):
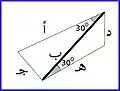
أريد أن انظر الآن إلى الخط من زاوية أخرى للتوضيح (في الرسمات التي تليها سيتم النظر من المنظور الجديد للتوضيح فقط -وسنترك المسقط العلوي ) أطوال الأضلاع ب، ج هي: ب= أ جتا30° ج= أ جا30°
ثم نأتي إلى الدوران الثاني:
والذي نريد فيه تحليل ب إلى مركبتين
نظلل الخط المعني هنا وهو ب ولنسم المركبتين الوهميتين له بـ هـ، د
حيث: هـ = ب جتا30° , د = ب جا30° , سنرى لاحقاً أن الخط هـ لن يظهر عند النظر إلى المكعب من المسقط العلوي
لاحظ أن الدوران الثاني كان حول الضلع ج وبالتالي لا يتغير الضلع ج بتاتاً (طولاً ولا اتجاهاً) وبالتالي لا توجد له مركبات.
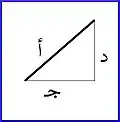
نعود إلى المسقط الأمامي
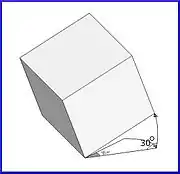
إذاً . . . هكذا تم التدوير (لا تخلط بين الرسمة التالية والرسمات السابقة، المنظور هنا يختلف للتوضيح):
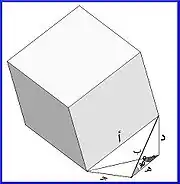
وهكذا تم التحليل:
وبالتالي يمكن رسم الضلع برسم ضلعين قائمين الأول ج وطوله أ جا30 والثاني د وطوله ب جا30° = أ جتا30° جا30° ومن ثم نصل بينهما كما في الشكل:
أنهينا رسم الضلع الأول . . . جيد جداً, تأكد أنك فهمت السابق بشكل جيد ولا تكمل إن وجد أي خلل في الفهم لأنه حوالي 80% من الذي تحتاجه لفهم الموضوع)
إن أتممت الفهم . . . أكمل التالي
رسم الخط القائم أمام الناظر أصلاً
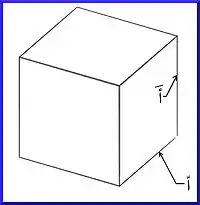
نعود للمسقط الأمامي ونأتي إلى الضلع الثاني في المكعب ولنسمه أَ
نكرر الخطوات السابقة كالتالي:
أولاً ومع الدورة 1: دورنا الجسم مع عقارب الساعة عند النظر إليه من أعلى كما في الشكل التوضيحي للدوران - في الأعلى-.... هنا دار الضلع أولاً حول محوره وبالتالي لم يتغير طوله ولا اتجاهه، فلا نرسم مركبات.
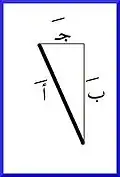
ثم دار الضلع 30° عكس عقارب الساعة عند النظر إليه من الجانب الأيمن
انظر الرسم التالي من المسقط الجانبي الأيمن لاحظ أن الخط الوهمي جَ لن يظهر من المسقط الأمامي ولا شيء يعتمد عليه وبالتالي لا داعي لحسابها، أما بَ فطولها =أَ جتا30° وطول بَ فقط هو الذي سيظهر من المسقط الأمامي وستظهر طبعاً كخط مستقيم عمودي لا مائل (وطوله يساوي طول بَ)
(علماً أنها حقيقة قد مالت ولكن هذا الميلان يؤثر على طولها، لا على اتجاهها).
رسم الخط المنبسط أمام الناظر أصلاً
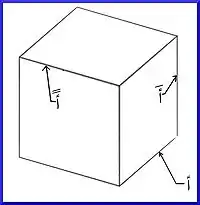
لنرسم الضلع أً والذي دار كما دار المكعب (مع عقارب الساعة عند النظر إليه من أعلى، وعكس عقارب الساعة عند النظر إليه من الجانب الأيمن) وبما أنك استوعبت الطريقة الآن، لن أسهب في شرح كيفية الدوران . . . .
ببساطة، كل ما نفعله هو أن نرسم مركبتين متعامدتين . . . . . السينية طولها أً جتا30 باتجاه (س-) (اليسار) بالنسبة لصفحة الرسم . . . . . والصادية طولها أًجا² 30° باتجاه (ص+) (الأعلى) بالنسبة لصفحة الرسم
وهكذا أنهينا رسم كل الخطوط في المكعب (الأضلاع الباقية موازية لإحدى التي رسمناها، لا تحتاج إلى إعادة تفكير) وأفضل طريقة لرسم الخطوط الأخرى: وهي أن تبقي حساباتك لكل خط على ورقة جانبية، وترسم وفقاً لهذه الحسابات (كل خط ترسم الموازي له بنفس حسابات الأول).
قد تبدو الطريقة بسيطة ولا حاجة لهذه الخطوات كلها، وإنما يزداد التعقيد عندما ترسم مجسما يكون مائلاً أصلاً أو تريد تدويره بعدد دوراتٍ أكثرَ من 2 (وهو عدد الدورات التي دورنا بها المجسم هنا)
بقي أمر أخير، وهو الأضلاع التي تكون مائلة أصلاً (شيء غير المكعب) مثل أي بلورة أو هرم نعتبر الميلان وكأنه تدوير أول، ونضع له مركبتين، ونراعي تدوير المركبات الناتجة كما فعلنا هنا.
بوابة هندسة تطبيقية
بوابة رياضيات